
图1 风电经柔直并网的系统结构
Fig.1 Structure of wind farms integration through flexible HVDC
Mechanism Analysis and Risk Assessment of Broadband Resonance in Doubly-fed Induction Generator-based Wind Farms Integration Through Flexible HVDC
柔性直流输电(flexible high voltage direct current transmission,flexible HVDC)技术由于具有结构灵活、可控性高、输出谐波小等特点,已成为风电大规模远距离输送的理想方式[1-3]。但是,在孤岛送出模式下,柔直换流站与风电场相互作用可能引发新型的振荡问题。2013年,中国广东南澳柔性直流输电线路在风电场出力逐渐增大的过程中曾出现频率在20~30 Hz的振荡现象[4-5]。2014年,德国北海海上风电场经柔性直流线路送出时发生过更为严重的振荡,振荡频率在250~350 Hz,振荡电流达到基波电流的40%以上[6]。
在振荡发生初期,有学者侧重于对振荡电流分量在系统中分布及传播机制的研究[7],而对引发振荡的根源难以解释清楚。随着阻抗分析法[8]的广泛应用,振荡的频率、阻尼及稳定性从频域阻抗特性的角度得以诠释。不同于传统的电力系统振荡形态,这种新型的振荡形态源于电力电子变流器之间相互作用产生的机网耦合振荡,往往难以从机组或电网侧找到初始的固有振荡模态,振荡的发生常与电力电子装置控制参数强相关[9-10]。
文献[11]仿真了在风机变流器和柔直换流器两者控制参数失配情况下发生次/超同步频率范围的振荡现象,通过风机变流器和柔直换流器两者控制带宽比与等效阻抗的关系,解释了这一现象的成因。文献[12]分析了风机锁相环参数对柔直送出系统发生次/超同步振荡的影响,并通过优化锁相环参数改善风机等效阻抗,降低系统振荡风险。文献[13-14]深入研究了直驱风电场与柔直互联系统发生次同步振荡的原因及抑制方法。上述文献均并未涉及发生中高频振荡(100 Hz以上)的研究。
文献[15]较为全面地研究了双馈/直驱风电机组与柔直换流站的宽频阻抗特征,分析了关键控制参数对互联系统引发宽频振荡风险的影响。受风速、并网风机台数等外部条件的综合影响,风机与柔直互联系统可能发生更为复杂的宽频振荡问题。文献[16-17]利用特征值分析法和阻抗分析法解释了改变风机台数后风电经柔直并网系统出现400多Hz振荡的原因,指出系统振荡频率呈现负阻尼特性。目前,风电经柔直并网系统发生的宽频带振荡在不同频段下的综合影响因素及作用机理仍有待深入研究。
本文以双馈风力发电机组为例,研究风电与柔直相互作用引发的系统振荡问题。首先,介绍了双馈风机经柔性直流输电并网仿真模型,搭建了基于风机控制器在环的RT-Lab实时仿真系统。以基于扫频的阻抗测量为手段,确立了适用于研究对象振荡分析的阻抗模型。利用网络阻尼判据,从子系统等效阻感、阻容的特性,分析了互联系统发生次/超同步、中高频振荡的机理。然后,将发生振荡的宽频带分为次/超同步频段、中频段(100~500 Hz)和高频段(500 Hz以上),考虑风机控制、柔性直流控制以及风速和并网风机台数的影响,分别分析不同频段下振荡的阻抗特性,并利用聚合RLC电路法量化影响因素变化对潜在振荡风险、潜在振荡频率的影响。最后,归纳总结了双馈风电场经柔性直流并网系统在不同频段范围发生振荡的关键影响因素。
1.1.1 整体模型
风电经柔性直流并网的典型拓扑如图1所示。图1中,柔性直流输电系统为两端MMC-HVDC结构,其额定直流电压为500 kV,额定传输容量为1500 MW,柔直换流器、换流变、直流线路等一次参数参照文献[18]中系统参数进行设置;风电场由1.5 MW的双馈风机倍乘等值建模,通过0.69 kV/35 kV箱变、35 kV/230 kV升压站以及汇集线路接入公共连接点(point of common coupling,PCC);受端交流电网可利用戴维南等值建模实现。双馈风电机组控制部分采用风机变流器控制器真实设备接入的方式,柔直换流控制部分采用典型控制数学模型搭建的方式。

图1 风电经柔直并网的系统结构
Fig.1 Structure of wind farms integration through flexible HVDC
1.1.2 柔性直流换流站控制模型
双端柔性直流输电系统换流站均采用MMC结构。送端换流站MMC1负责控制风电场公共耦合点交流电压的幅值和频率,为风电场提供稳定的交流电源;受端换流站MMC2负责控制直流母线电压稳定,同时能够向交流电网提供一定的无功功率。送端换流站运行在孤岛控制模式,内外环的主控制器采用dq解耦控制,其控制结构如图2所示。

图2 MMC送端换流站控制结构
Fig.2 Control structure of MMC sending-end converter station
1.1.3 整体系统仿真构架
基于RT-Lab建立风电场经柔直并网系统实时仿真平台,如图3所示。柔直主电路与极控系统采用CPU模型,共占用4个CPU核(1台OP5600);换流站阀体及阀控采用FPGA模型,共占用4个Xilinx VC707卡(4台OP5607);风机主电路和风机变流器分别采用CPU模型和FPGA模型(1台OP5700),与变流控制器实物相连接。
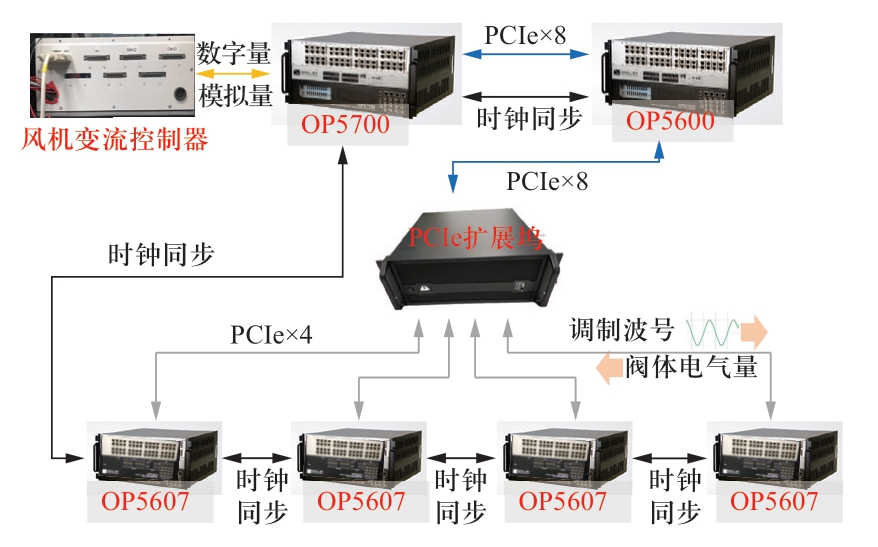
图3 风电经柔直并网系统实时仿真平台
Fig.3 Real-time simulation platform of wind farms integration through flexible HVDC
为分析这种互联系统发生宽频带振荡问题,在关注工况的稳态运行点建立基于频域阻抗的小信号模型。对于风机或MMC的“白箱”系统,采用机理建模法得到出口处电压Δui和电流Δii的关系[13]。而对于“黑箱”系统可根据实验测量数据利用模型辨识法[19]得到序阻抗模型。
以PCC点为界,图1所示的互联系统可分为风机侧子系统和柔直侧子系统,其等效序阻抗模型如图4所示。其中,柔直侧子系统等效为电压源UM和等效阻抗ZM,ZM包含换流站阻抗ZMMC和换流变阻抗ZT;风机侧子系统等效为电流源Iw和等效阻抗Zw,Zw包括风机阻抗Zwind和汇集线路阻抗Zgrid。
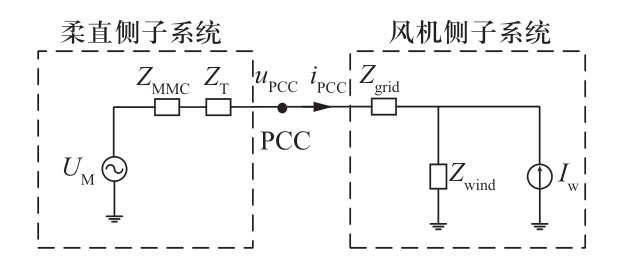
图4 风电经柔直并网系统等效阻抗模型
Fig.4 Equivalent impedance model of wind farms integration through flexible HVDC
风电机组变流器中的锁相环、直流母线外环控制等不对称控制,会导致注入扰动后产生与基频对称的镜像扰动响应,若不考虑频率耦合则无法准确求得序阻抗矩阵[15]。为此,采用成对频率扫描实验求解阻抗矩阵。
1)在某一频率及其镜像频率下分别进行扫频测试,由两次实验分别获得端口电压、电流中对应的扰动频率分量,如图5所示,其中两次扫频实验选择的频率点分别为f1和2f0-f1,如图5所示。
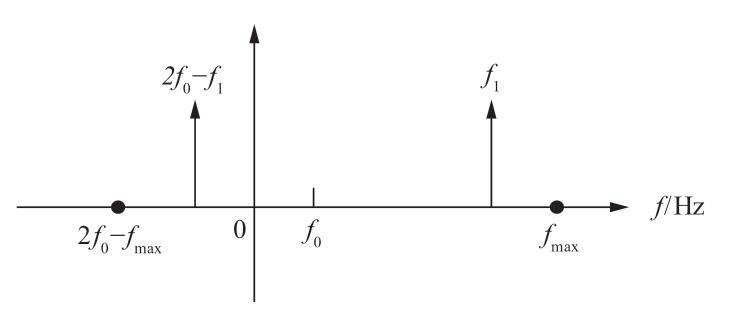
图5 扫频实验测试频率点
Fig.5 Tested frequency points of the sweep experiment
2)利用两次扫频实验获得的端口电压、电流及其扰动分量构成线性方程组
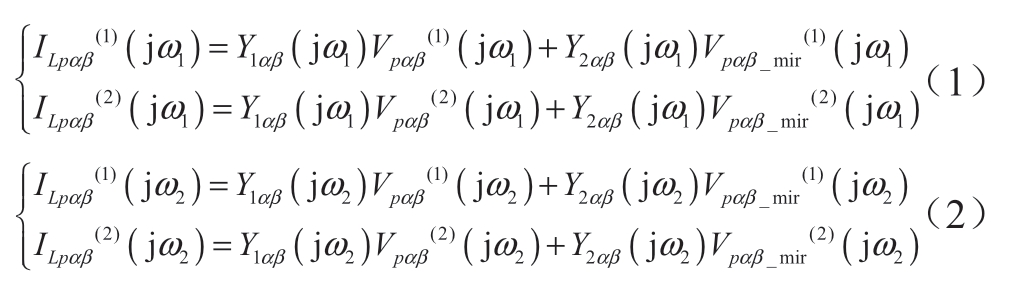
其中,Vpαβ(1)(jω1)和ILpαβ(1)(jω1)分别为注入扰动频率f1后获得的端口电压扰动、端口电流响应中对应频点f1的测量值,Vpαβ_mir(1)(jω1)为此时获得的端口镜像频率f2电压扰动信号的镜像量Vpαβ(2)(jω1)和ILpαβ(2)(jω1)分别为注入扰动频率f2后获得的端口电压扰动、端口电流响应中对应频点f1的测量值,Vpαβ_mir(2)(jω2)为此时获得的端口镜像频率f2电压扰动信号的镜像量。
3)经两次扫频实验,整理列出频点f1和频点f2导纳求解表达式
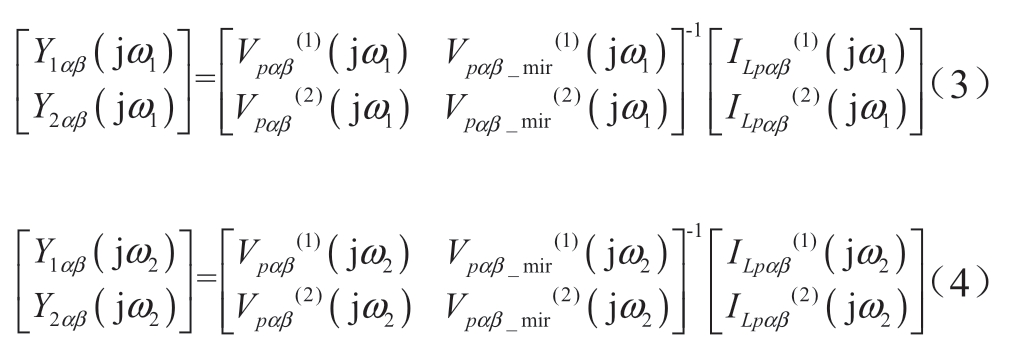
考虑多输入多输出(mutiple-input mutiple-output,MIMO)系统的广义奈奎斯特稳定性判据计算复杂且不便从物理意义直观解释,这里将非对角项折算到对角项阻抗中,修正后的正序阻抗Zp和负序阻抗Zn可表示为[20]:

基于频域阻抗的系统稳定性判据结合时域仿真验证,可较为充分地分析互联系统的振荡问题。由序阻抗的相角裕度判据或奈奎斯特判据,可推导出网络阻尼判据,即当XM(jω)+Xw(jω)=0ω,都有RΣ(jω)>0,即系统稳定。其中,RΣ(jω)=RM(jω)+Rw(jω)。
网络阻尼判据可理解为互联系统在谐振频率点若具有正阻尼,则系统稳定;若具有负阻尼,则系统存在振荡风险。网络阻尼判据体现出更直接的物理意义,并且根据子系统的阻尼特性可分辨其对引发振荡的贡献。
为了进一步实现对系统振荡风险量化评估,采用基于聚合RLC电路模型的振荡分析方法,即在振荡点附近,将系统聚合为串联二阶RLC电路,通过拟合技术得到等效电路参数,利用等效电路的谐振阻尼σ和谐振频率ω对振荡风险量化评估,其计算公式如式(7)和(8)所示。
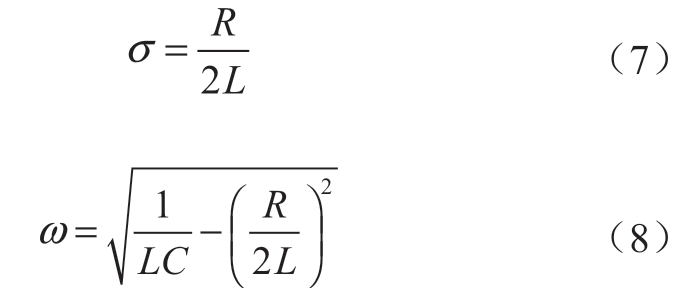
采用扫频测量和网络阻尼判据,图1系统中柔直送端并网900台风机满发时稳定工况的阻抗特性如图6(a)所示。由图6(a)可见,在等效电抗方面,风机侧系统在次/超同步频率范围呈现电感特性,在中高频段随着频率的提高逐渐转变为电容特性;柔直侧系统在次同步频率范围呈现电容特性,在超同步、中高频均呈现电感特性。在等效电阻方面,在次同步频率范围风机侧系统具有负电阻特性,频率非常高时柔直侧系统为负电阻特性,除此以外,两者均为正电阻特性。
若在某一次/超同步频率下风机侧系统等效电感与柔直侧系统等效电容数值相同,具备LC谐振条件,而此频率下风机侧系统等效的负电阻绝对值大于柔直侧系统等效电阻值,则系统存在次/超同步振荡问题,如图6(b)和6(c)所示。
若在某一中高频率下风机侧系统等效电容与柔直侧系统等效电感数值相同,或是由于控制问题导致谐振峰的出现,使互联系统具备LC谐振条件,而此频率下风机侧系统或柔直侧系统变为负电阻特性,且绝对值大于对侧系统等效正电阻值,则系统存在中高频振荡问题,如图6(d)和6(e)所示。
因此,互联系统的振荡机理可以解释为:风机与柔直存在自身的LC特性,而在控制器的积极参与下,系统形成一定的振荡模式,同时诱发相应子系统的等效电阻的减小,导致在振荡点的互联系统等效电阻为负,从而引发不稳定振荡。
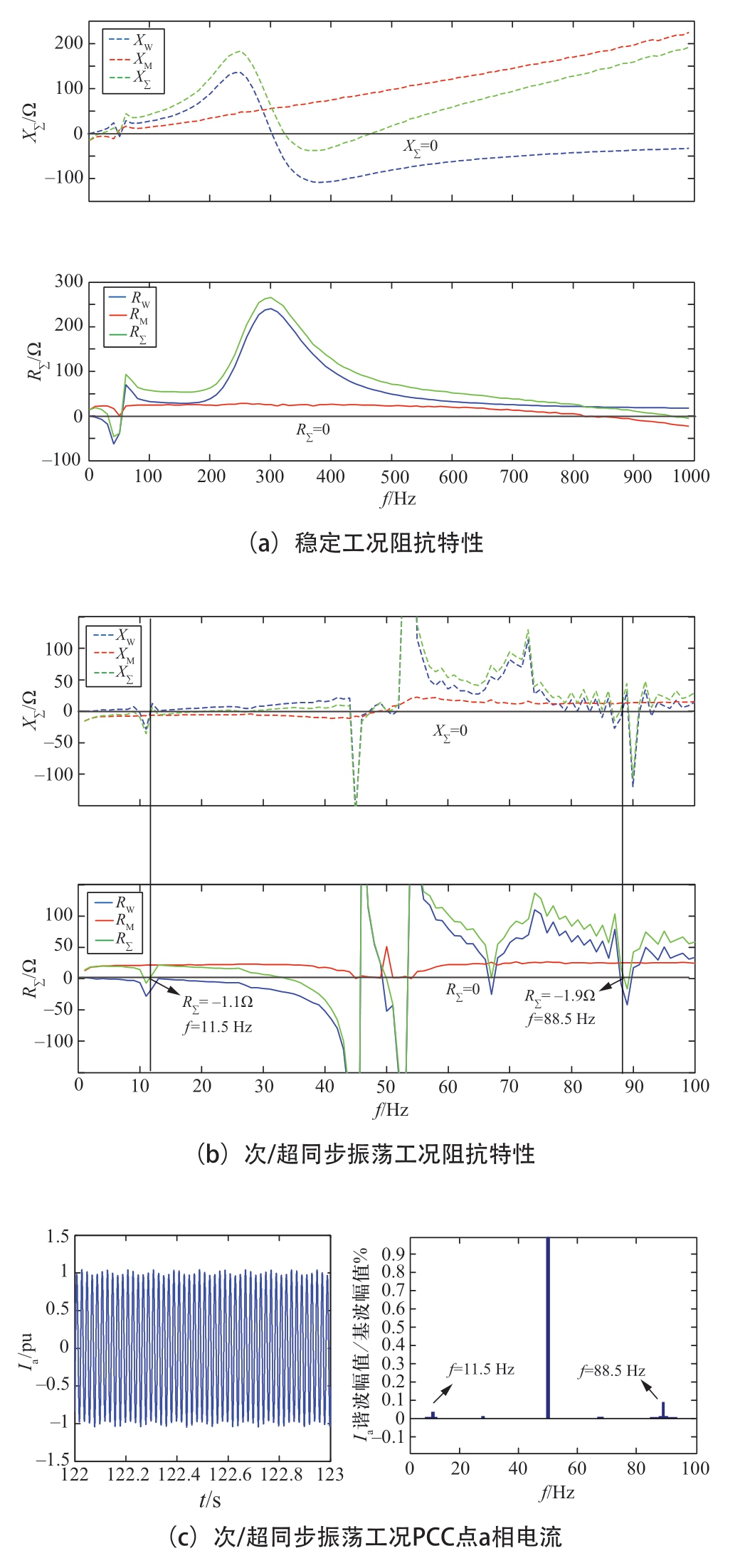
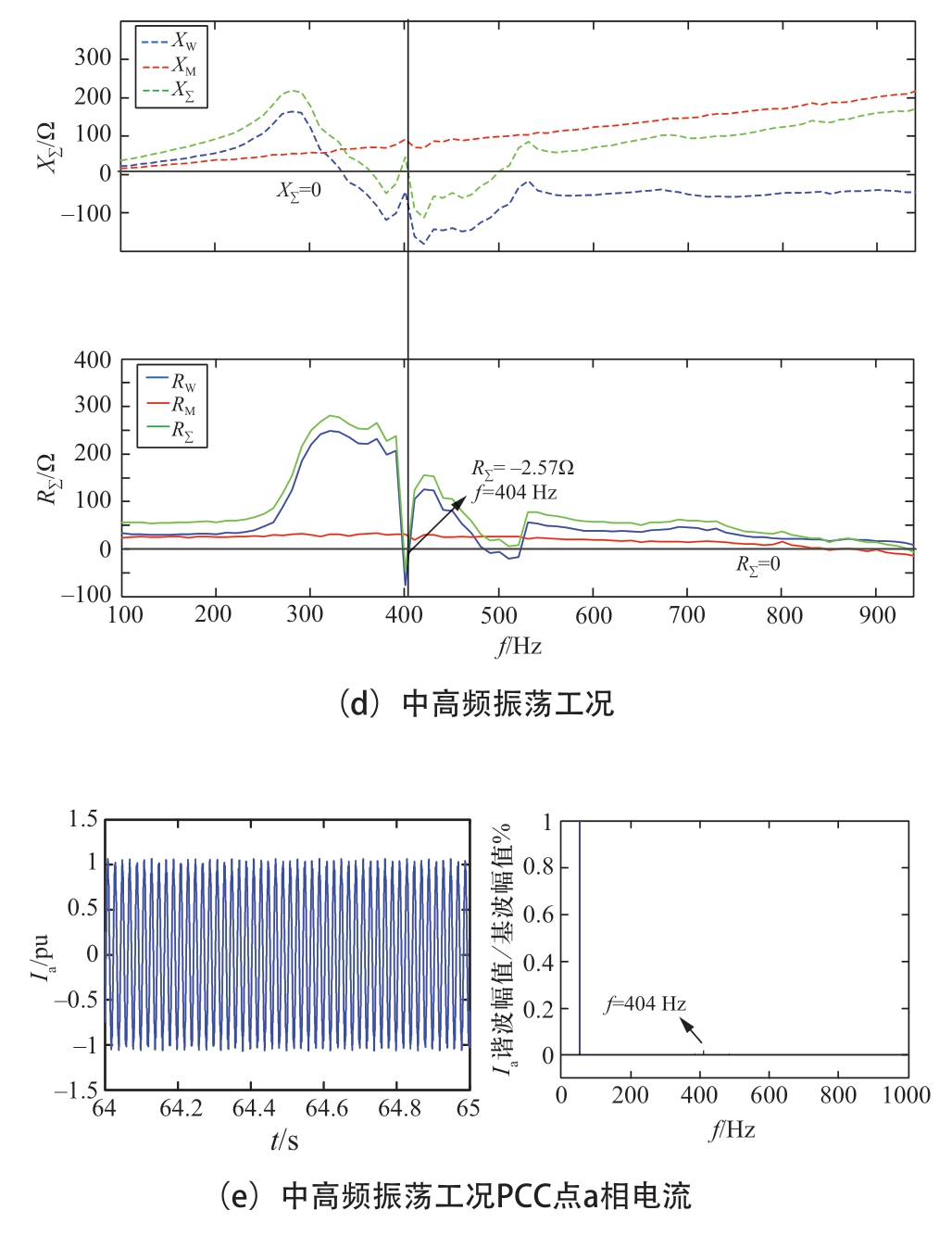
图6 系统频域阻抗特性与时域仿真结果
Fig.6 Impedance characteristics in frequency domain and simulation results in time domain
风机网侧、机侧变流器控制参数及锁相环控制参数、MMC控制参数设置不当时,互联系统会产生次/超同步频率的振荡问题。本节利用网络阻尼判据与聚合RLC电路法,对影响因素与振荡风险、振荡频率的关系进行分析。
3.1.1 风机网侧逆变器外环控制比例增益偏小情况
随着风机网侧逆变器外环控制比例增益的变小,互联系统等效阻抗会在10 Hz和90 Hz附近呈现负阻尼特性的谐振点,如图7(a)所示。为在谐振点附近拟合二阶RLC电路,在9~12 Hz范围以0.1 Hz频率间隔详细扫描阻抗特性,如图7(b)所示。可见,外环控制比例增益Kpgo取0.4时,等效电抗曲线过零处,等效电阻为正值,系统处于稳定状态。当Kpgo减小到0.3时,谐振点对应等效电阻为负值,系统存在振荡风险。
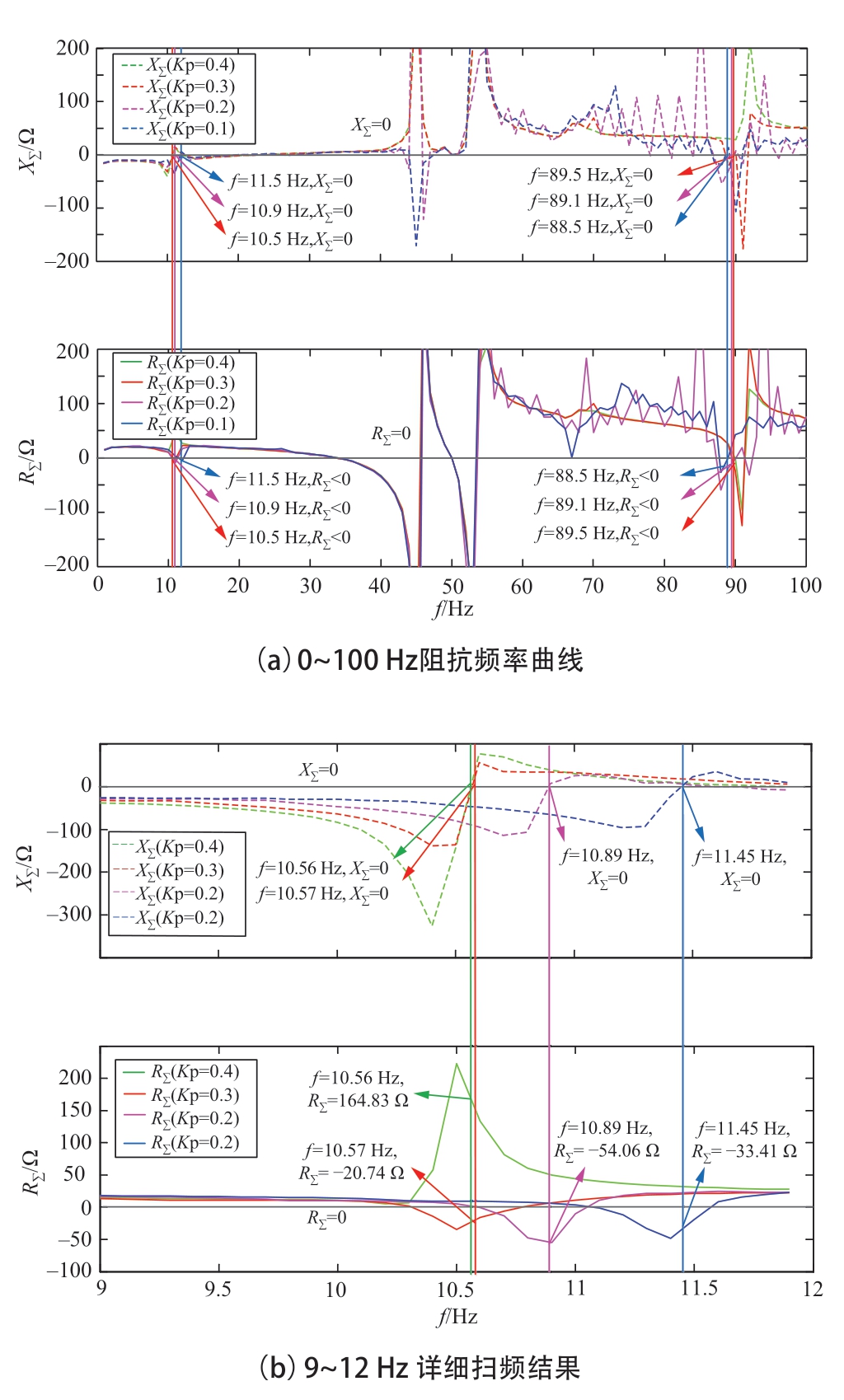
图7 风机网侧逆变器外环比例增益偏小时的阻抗特性
Fig.7 Impedance characteristics in the condition of smaller proportional gain in the outer loop of wind generator grid side converter
对10 Hz振荡频率附近进行RLC电路拟合,拟合结果如表1所示。由表1可知,随着Kpgo的减小,系统从稳定进入到振荡状态,谐振阻尼逐渐减小,振荡风险加剧,振荡频率在10 Hz附近略有提升。
表1 风机网侧逆变器外环比例增益偏小时RLC拟合结果
Table1 RLC fitting results in the condition of smaller proportional gain in the outer loop of wind generator grid side converter
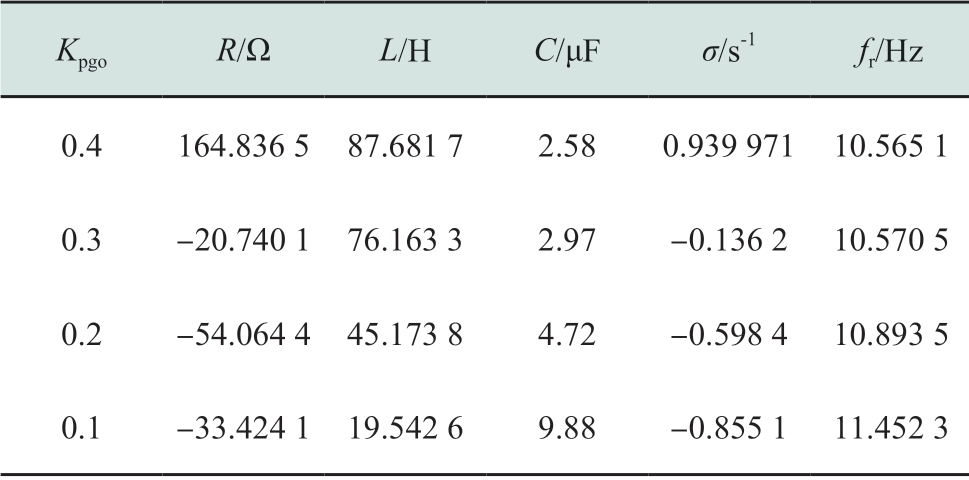
KpgoR/ΩL/HC/μFσ/s-1fr/Hz 0.4 164.836 5 87.681 7 2.58 0.939 971 10.565 1 0.3 -20.740 1 76.163 3 2.97 -0.136 2 10.570 5 0.2 -54.064 4 45.173 8 4.72 -0.598 4 10.893 5 0.1 -33.424 1 19.542 6 9.88 -0.855 1 11.452 3
3.1.2 风机网侧逆变器内环控制比例增益偏小情况
随着风机网侧逆变器内环控制比例增益的变小,互联系统等效阻抗会在20~35 Hz附近呈现负阻尼特性的谐振点,如图8所示。内环控制比例增益Kpgi取0.25时,系统无潜在谐振模态,系统处于稳定状态。当Kpgi减小到0.24时,谐振点对应等效电阻为负值,系统存在振荡风险。
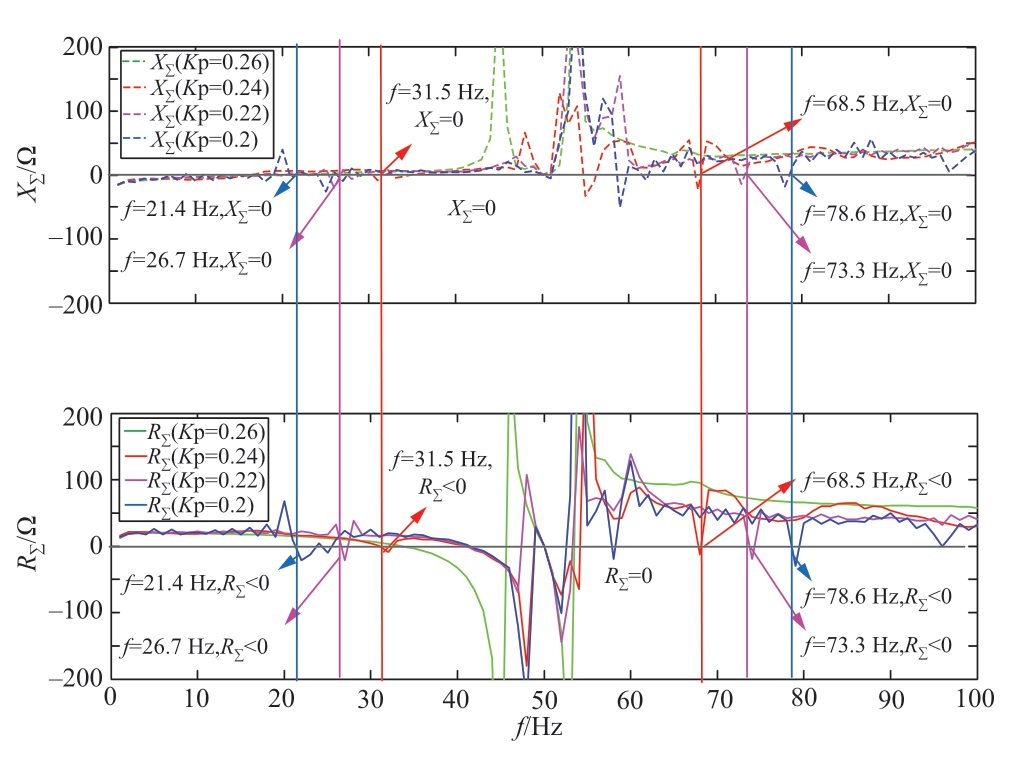
图8 风机网侧逆变器内环比例增益偏小时的阻抗特性
Fig.8 Impedance characteristics in the condition of smaller proportional gain in the inner loop of wind generator grid side converter
同样对次同步振荡频率附近进行RLC电路拟合,拟合结果如表2所示。由表2可知,随着Kpgi的减小,系统从稳定进入到振荡状态,谐振阻尼逐渐减小,振荡风险加剧,振荡频率逐渐减小。
表2 风机网侧逆变器内环比例增益偏小时RLC拟合结果
Table2 RLC fitting results in the condition of smaller proportional gain in the inner loop of wind generator grid side converter
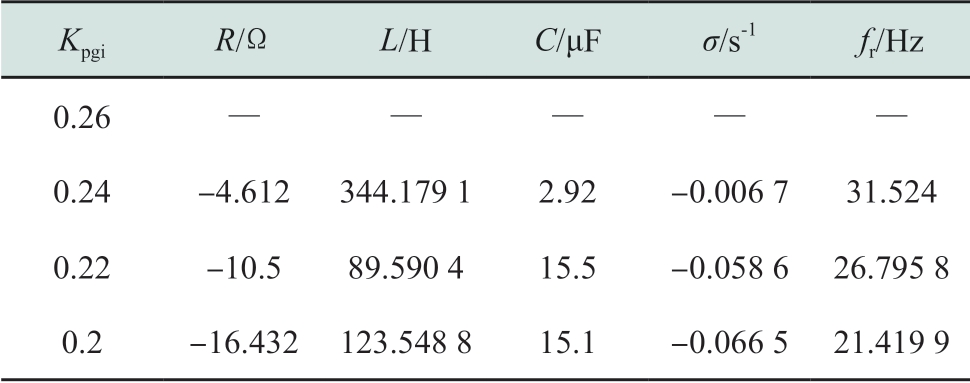
KpgiR/ΩL/HC/μFσ/s-1fr/Hz 0.26— —0.24 -4.612 344.179 1 2.92 -0.006 7 31.524 0.22 -10.5 89.590 4 15.5 -0.058 6 26.795 8 0.2 -16.432 123.548 8 15.1 -0.066 5 21.419 9
3.1.3 风机机侧变流器外环控制比例增益偏小情况
随着风机机侧变流器外环控制比例增益的变小,互联系统等效阻抗会在8 Hz附近呈现负阻尼特性的谐振点,如图9所示。内环控制比例增益Kpro取0.5时,系统无潜在谐振模态,系统处于稳定状态。当Kpro减小到0.3时,谐振点对应等效电阻为负值,系统存在振荡风险。
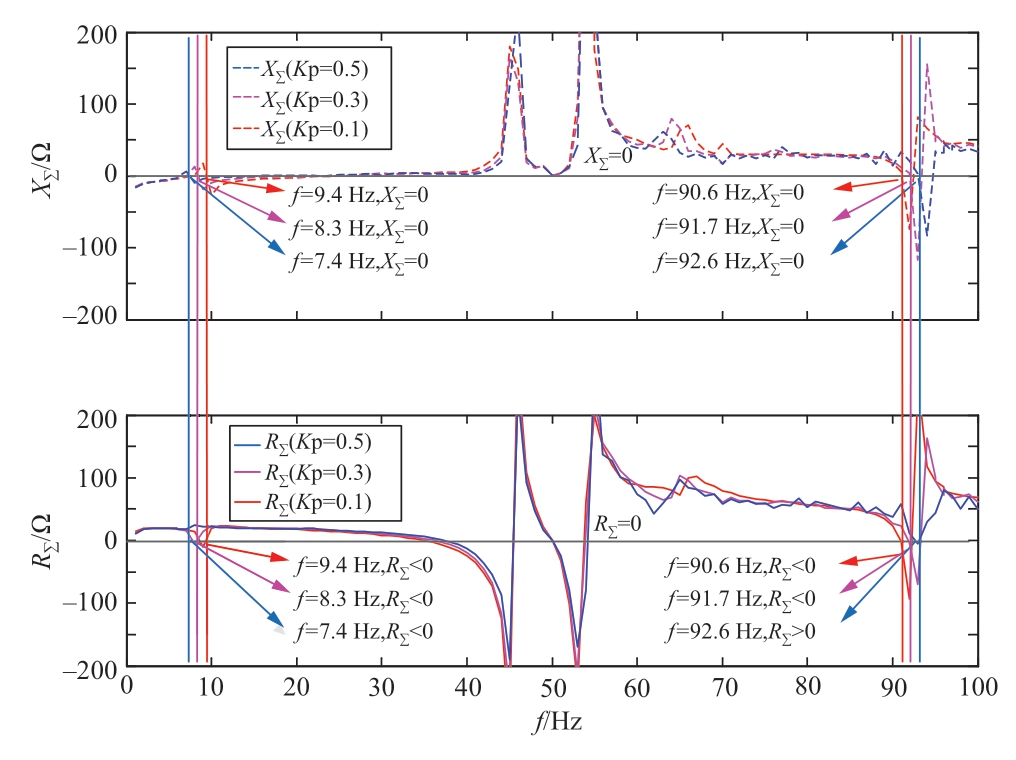
图9 风机机侧变流器外环比例增益偏小时的阻抗特性
Fig.9 Impedance characteristics in the condition of smaller proportional gain in the outer loop of wind generator machine side converter
同样对8 Hz振荡频率附近进行RLC电路拟合,拟合结果如表3所示。由表3可知,随着Kpro的减小,系统从稳定进入到振荡状态,谐振阻尼逐渐减小,振荡风险加剧,振荡频率略有提升。
表3 风机机侧变流器外环比例增益偏小时RLC拟合结果
Table3 RLC fitting results in the condition of smaller proportional gain in the outer loop of wind generator machine side converter
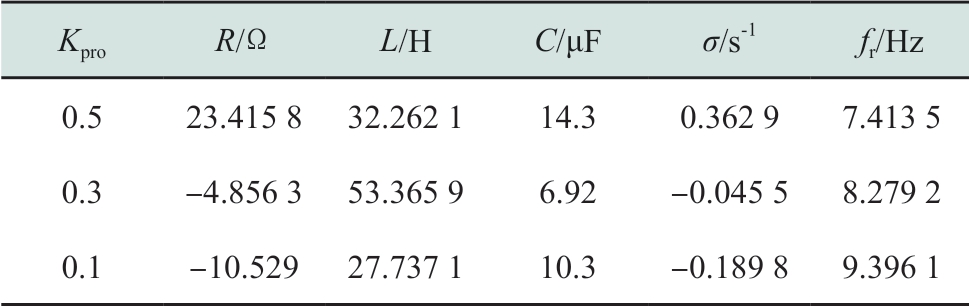
KproR/ΩL/HC/μFσ/s-1fr/Hz 0.5 23.415 8 32.262 1 14.3 0.362 9 7.413 5 0.3 -4.856 3 53.365 9 6.92 -0.045 5 8.279 2 0.1 -10.529 27.737 1 10.3 -0.189 8 9.396 1
3.1.4 MMC外环控制比例增益偏小情况
经阻抗分析,MMC外环控制比例增益偏小会使得互联系统等效阻抗在40 Hz附近出现负阻尼特性的谐振点。对振荡频率附近进行RLC电路拟合,拟合结果如表4所示。由表4可知,随着Kpmo的减小,系统从稳定进入到振荡状态,谐振阻尼逐渐减小,振荡风险加剧,振荡频率在40 Hz附近逐渐减小。
表4 MMC外环控制比例增益偏小时RLC拟合结果
Table4 RLC fitting results in the condition of smaller proportional gain in the outer loop of MMC
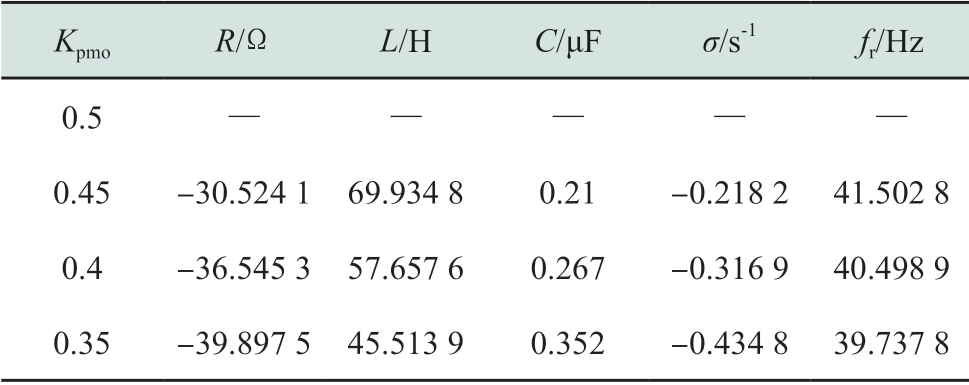
KpmoR/ΩL/HC/μFσ/s-1fr/Hz 0.5— —0.45 -30.524 1 69.934 8 0.21 -0.218 2 41.502 8 0.4 -36.545 3 57.657 6 0.267 -0.316 9 40.498 9 0.35 -39.897 5 45.513 9 0.352 -0.434 8 39.737 8
3.1.5 风机锁相环控制比例增益偏大情况
随着风机锁相环控制比例增益的变大,互联系统等效阻抗会在40~60 Hz呈现负阻尼特性的谐振点。经阻抗分析可得:随着锁相环控制比例增益的变大,系统从稳定进入到振荡状态,谐振阻尼逐渐减小,振荡风险加剧。
风机网侧逆变器内环控制比例增益偏大时,互联系统易产生中频振荡现象。而受风速影响,系统存在更宽频带的中频振荡风险。
3.2.1 风机网侧逆变器内环控制比例增益偏大情况
经阻抗分析,风机网侧逆变器内环控制比例增益偏大会使得互联系统等效阻抗在400 Hz周围出现负阻尼特性的谐振点。对振荡频率附近进行RLC电路拟合,拟合结果如表5所示。可见,随着Kpgi的增大,系统从稳定进入到振荡状态,谐振阻尼逐渐减小,振荡风险加剧,振荡频率在400 Hz附近逐渐提升。
表5 风机网侧逆变器内环比例增益偏大时RLC拟合结果
Table5 RLC fitting results in the condition of bigger proportional gain in the inner loop of wind generator grid side converter
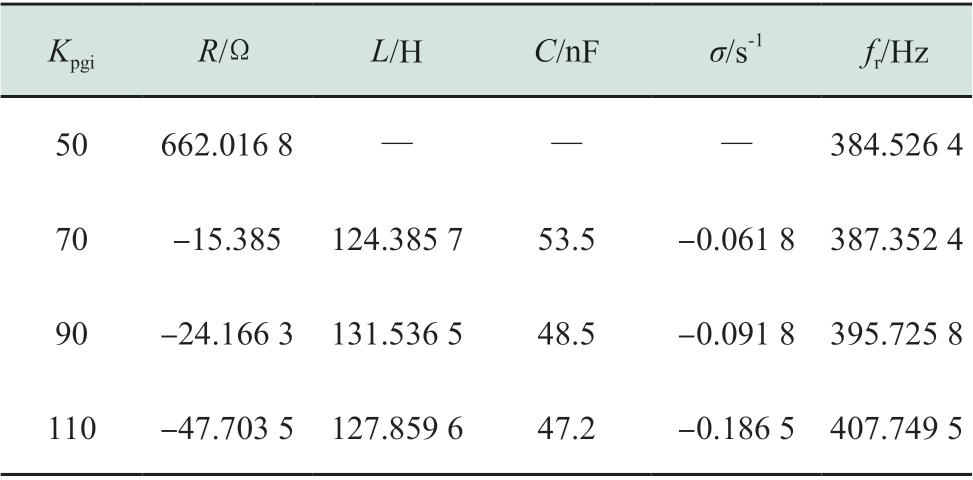
KpgiR/ΩL/HC/nFσ/s-1fr/Hz 50662.016 8— — —384.526 4 70 -15.385 124.385 7 53.5 -0.061 8 387.352 4 90 -24.166 3 131.536 5 48.5 -0.091 8 395.725 8 110 -47.703 5 127.859 6 47.2 -0.186 5 407.749 5
3.2.2 风速的叠加影响
在风机内环控制器比例参数偏大的情况下,若叠加风速的变化,当风机出力变小时,互联系统会诱发更宽频带的振荡风险,阻抗特性如图10所示。可见,在额定运行风速(即出力1 pu)时,等效电抗曲线过0的潜在谐振点处,等效电阻为正,系统处于稳定状态;出力降至0.75 pu时,系统在372 Hz附近出现负阻尼振荡点;出力降至0.5 pu时,系统在315 Hz和133 Hz附近出现负阻尼振荡点;出力降至0.25 pu时,系统在468 Hz、280 Hz以及119 Hz附近出现负阻尼振荡点,呈振荡模态增多且振荡频率范围变宽的趋势。
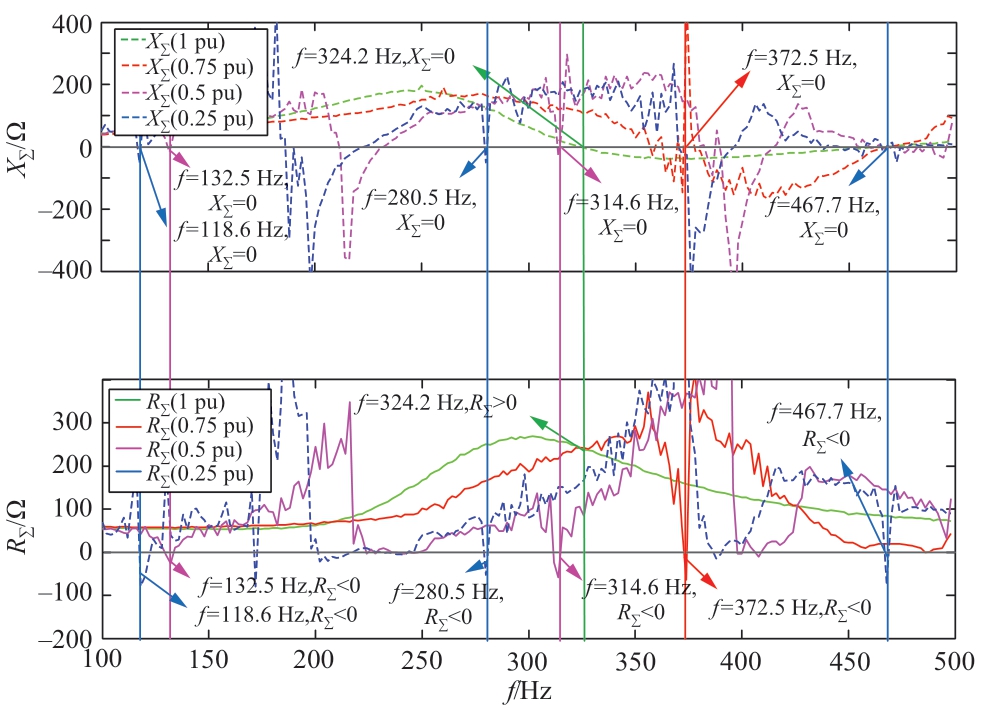
图10 考虑风速变化的阻抗特性
Fig.10 Impedance characteristics varying with wind speed variation
同样对各振荡频率附近进行RLC电路拟合,拟合结果如表6所示。可见,当风机网侧逆变器内环比例增益偏大并叠加风速的影响,系统谐振阻尼随风速降低而逐渐减小,振荡风险加剧。
表6 考虑风速变化时的RLC拟合结果
Table6 RLC fitting results varying with wind speed variation
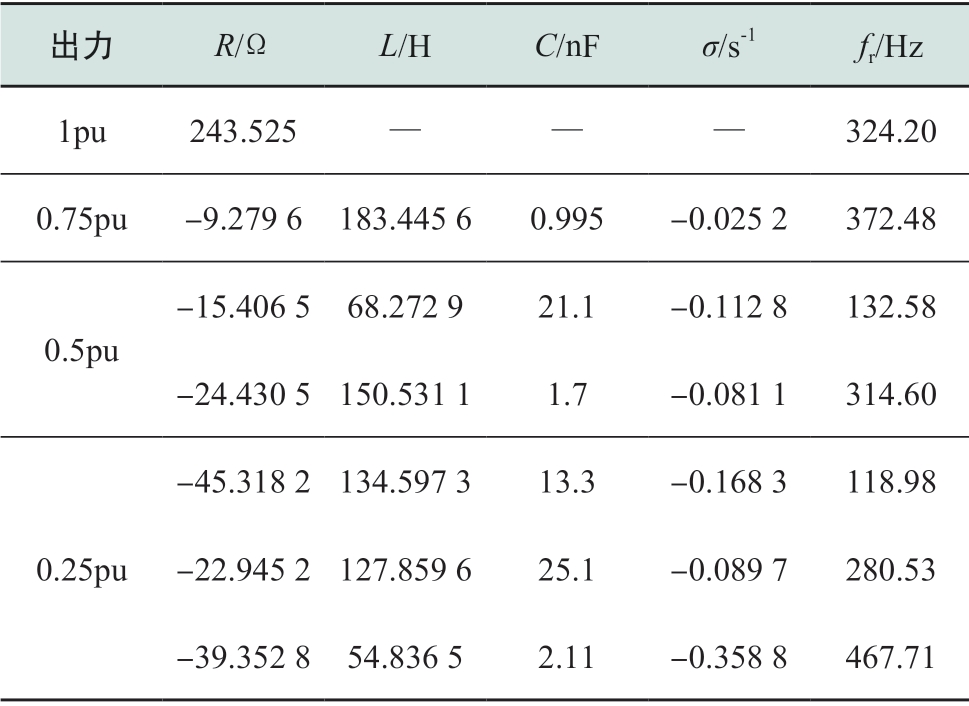
出力R/ΩL/HC/nFσ/s-1fr/Hz 1pu243.525— — —324.20 0.75pu -9.279 6 183.445 6 0.995 -0.025 2 372.48 0.5pu-15.406 5 68.272 9 21.1 -0.112 8 132.58-24.430 5 150.531 1 1.7 -0.081 1 314.60 0.25pu-45.318 2 134.597 3 13.3 -0.168 3 118.98-22.945 2 127.859 6 25.1 -0.089 7 280.53-39.352 8 54.836 5 2.11 -0.358 8 467.71
送端MMC内环控制器比例增益偏大时,互联系统易产生高频振荡现象。而受并网风机台数的影响,系统存在更宽频带的高频振荡风险。
3.3.1 MMC内环控制器比例增益偏大情况
经阻抗分析,MMC内环控制器比例增益偏大会使得互联系统等效阻抗在500~600 Hz出现负阻尼特性的谐振点。对振荡频率附近进行RLC电路拟合,拟合结果如表7所示。可见,随着Kpmi的增大,系统从稳定进入到振荡状态,谐振阻尼逐渐减小,振荡风险加剧,振荡频率有近100 Hz的提升。
表7 MMC内环控制器比例增益偏大时RLC拟合结果
Table7 RLC fitting results in the condition of bigger proportional gain in the inner loop of MMC
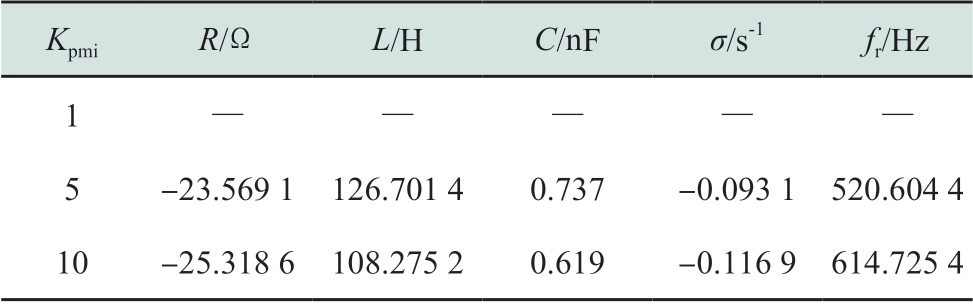
KpmiR/ΩL/HC/nFσ/s-1fr/Hz 1— —5 -23.569 1 126.701 4 0.737 -0.093 1 520.604 4 10 -25.318 6 108.275 2 0.619 -0.116 9 614.725 4
3.3.2 并网风机台数的叠加影响
在送端MMC内环控制器比例参数偏大的情况下,若叠加并网风机台数的变化,互联系统会诱发更宽范围的高频振荡风险,阻抗特性如图11所示。可见,在并网风机台数为400台时,系统处于稳定状态;当风机台数增多到600台时,在693 Hz附近出现负阻尼振荡点;随着风机台数的进一步增多,振荡频率降低,当增至1000 台时,振荡频率降至523 Hz。
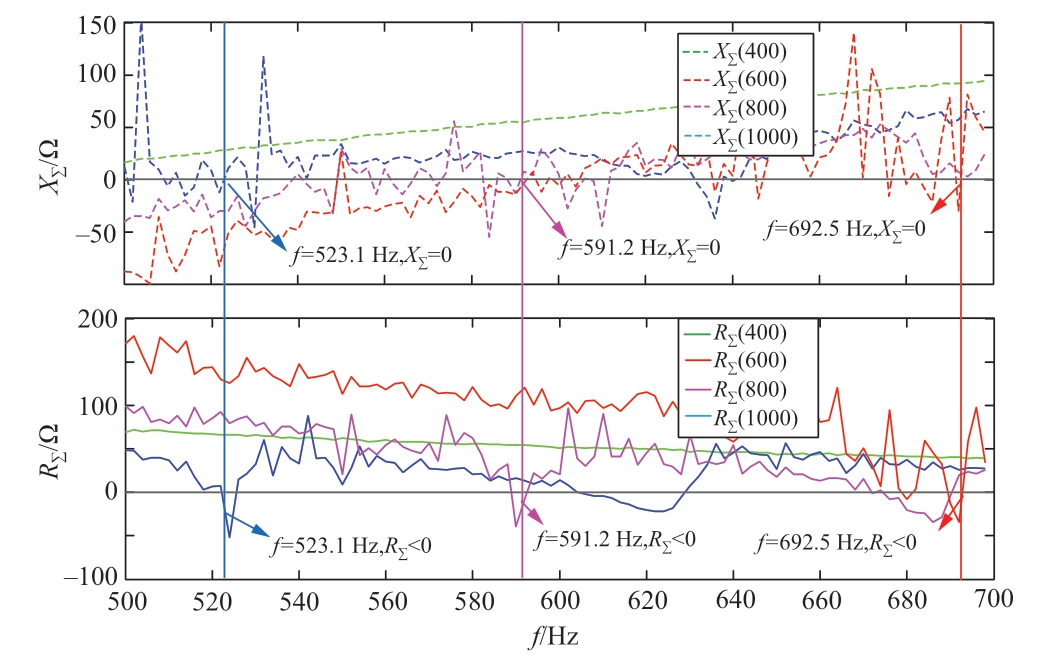
图11 考虑并网风机台数的阻抗特性
Fig.11 Impedance characteristics varying with number of gridconnected wind generators
对振荡频率附近进行RLC电路拟合,拟合结果如表8所示。可见,当送端MMC内环控制器比例增益偏大并叠加并网风机数量的影响,系统谐振阻尼随风机台数增多而逐渐减小,振荡风险加剧,振荡频率在高频范围内逐渐降低。
表8 考虑并网风机台数的RLC拟合结果
Table8 RLC fitting results varying with number of grid-connected wind generators
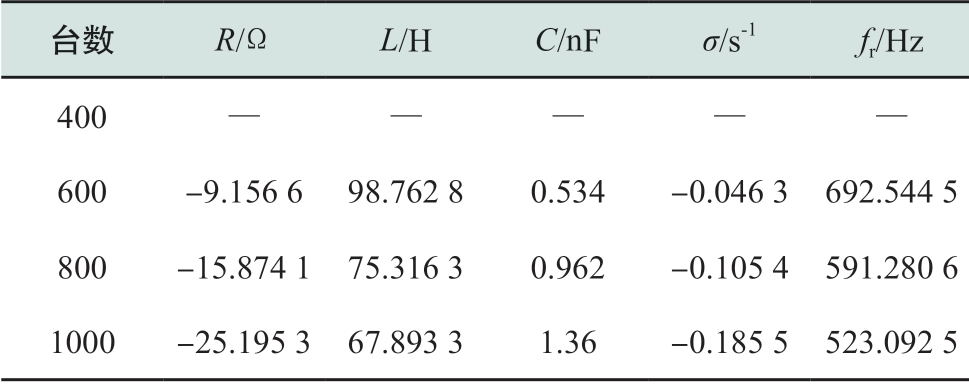
台数R/ΩL/HC/nFσ/s-1fr/Hz 400— —600 -9.156 6 98.762 8 0.534 -0.046 3 692.544 5 800 -15.874 1 75.316 3 0.962 -0.105 4 591.280 6 1000 -25.195 3 67.893 3 1.36 -0.185 5 523.092 5
综合次/超同步频率、中频、高频的振荡情况,考虑风机变流器及锁相环控制、MMC控制的影响与风速、并网风机台数的变化,多种因素对风机与柔直互联系统振荡风险的影响各不相同,其分别影响的主要频带如图12所示。
由图12可以看出,潜在振荡频率在20 Hz以内时,影响振荡的关键因素为双馈风机机/网侧变流器外环控制设置偏小,相应频率耦合产生与工频对称的80~100 Hz超同步电流分量。潜在振荡频率在20~40 Hz时,影响振荡的关键因素为双馈风机网侧变流器内环控制设置偏小或者MMC外环控制设置偏小,其中风机控制会耦合产生60~80 Hz超同步电流分量。潜在振荡频率在40~50 Hz时,影响振荡的关键因素为锁相环控制或MMC外环控制设置偏小,其中锁相环控制会耦合产生50~60 Hz超同步电流分量。
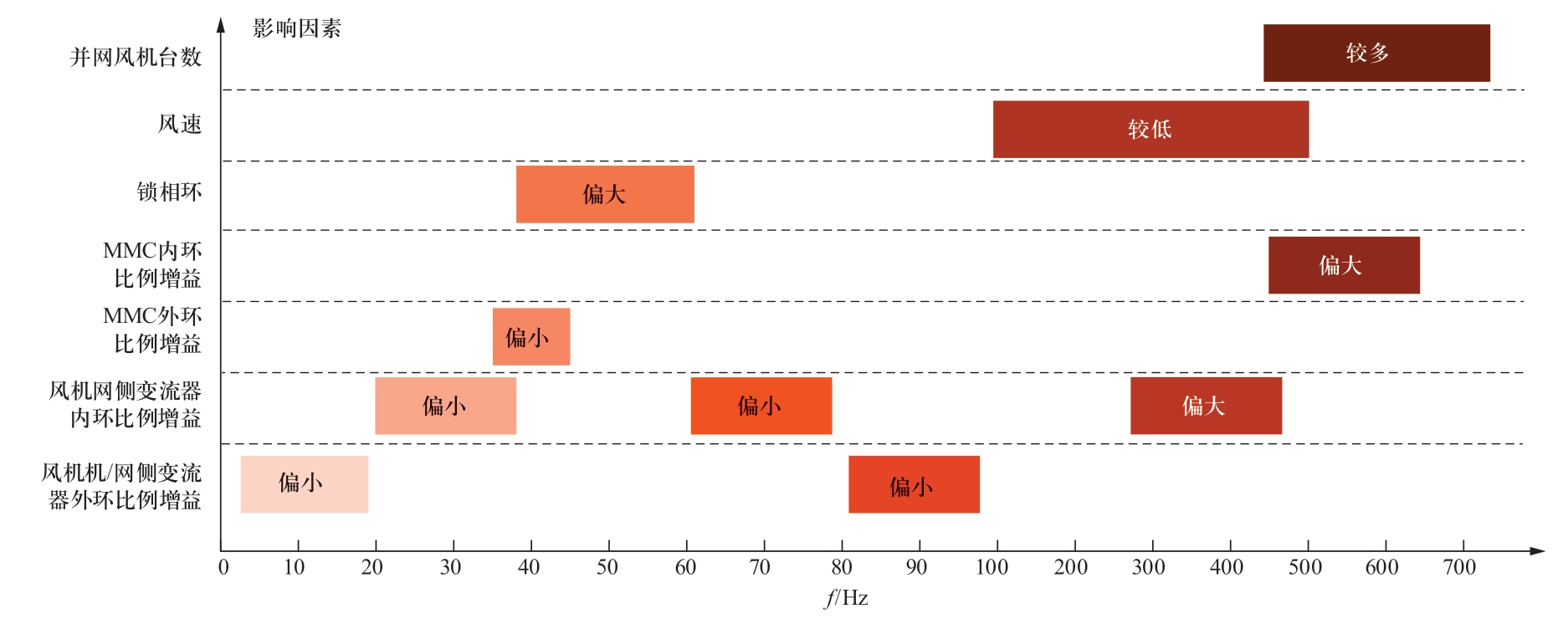
图12 各主要因素对不同频段振荡风险影响程度汇总
Fig.12 Summary of the influence of the main factors on the risk of oscillation in each frequency band
在中频段潜在振荡的关键因素是双馈风机网侧变流器内环控制设置偏大,若叠加低风速的影响,控制引发的振荡会更为严重,产生更多的振荡模态可能会覆盖整个中频段。
在高频段潜在振荡的关键因素是MMC内环控制设置偏大,当并网风机台数增加时,控制引发的振荡会更为严重,振荡频率会进一步提升。
本文以双馈风电场经MMC-HVDC并网系统为研究对象,从等效阻抗的角度分析了系统宽频带振荡机理,通过聚合阻抗量化评估了多种影响因素对不同频率范围的振荡风险,明确了系统宽频带振荡的关键影响因素,主要结论如下。
1)风机与柔性直流的控制系统相互作用是引发系统振荡的关键,风机与柔直存在自身的LC特性,在控制器的积极参与下,系统形成一定的振荡模式,同时诱发相应子系统等效电阻的减小而致使互联系统呈负阻尼,从而引发不稳定振荡。
2)风机变流器外/内环控制、送端MMC外环控制比例增益设置偏小或者锁相环比例增益设置偏大可能引发系统次/超同步振荡,其影响的潜在振荡频率由小及大。
3)风机网侧变流器内环控制比例增益设置偏大、MMC内环控制比例增益设置偏大可能会引发系统中、高频振荡,若叠加风速或风机台数的影响,控制引发的振荡将表现出更为宽泛的频率特征。
4)多种振荡影响因素的变化与振荡风险、振荡频率、阻尼存在较为明确的物理关系。
[1] 徐政,薛英林,张哲任.大容量架空线柔性直流输电关键技术及前景展望[J].中国电机工程学报,2014,34(29):5051-5062.
XU Zheng,XUE Yinglin,ZHANG Zheren.VSC-HVDC technology suitable for bulk power overhead line transmission[J].Proceedings of the CSEE,2014,34(29): 5051-5062(in Chinese).
[2] 郭贤珊,周杨,梅念,等.张北柔直电网的构建与特性分析[J].电网技术,2018,42(11):3698-3707.
GUO Xianshan,ZHOU Yang,MEI Nian,et al.Construction and characteristic analysis of Zhangbei flexible DC grid[J].Power System Technology,2018,42(11): 3698-3707(in Chinese).
[3] 肖晋宇,张宇,万磊,等.直流电网在全球能源互联网中的应用定位与案例研究[J].全球能源互联网,2018,1(1):32-38.
XIAO Jinyu,ZHANG Yu,WAN Lei,et al.Application of DC grid in global energy interconnection and case study[J].Journal of Global Energy Interconnection,2018,1(1): 32-38(in Chinese).
[4] 赵岩,郑斌毅,贺之渊.南汇柔性直流输电示范工程的控制方式和运行性能[J].南方电网技术,2012,6(6):6-10.
ZHAO Yan,ZHENG Binyi,HE Zhiyuan.The control mode and operating performance of Nanhui VSC-HVDC demonstration project[J].Southern Power System Technology,2012,6(6): 6-10(in Chinese).
[5] 魏伟,许树楷,李岩,等.南澳多端柔性直流输电示范工程系统调试[J].南方电网技术,2015,9(1):73-77.
WEI Wei,XU Shukai,LI Yan,et al.The system commissioning of Nan’ao VSC-MTDC demonstration project[J].Southern Power System Technology,2015,9(1): 73-77(in Chinese).
[6] Buchhagen C,Rauscher C,Menze A,et al.BorWin1-First Experiences with harmonic interactions in converter dominated grids[C]//International ETG Congress 2015; Die Energiewende- Blueprints for the new energy age; Proceedings of VDE,2016: 1-7.
[7] 吕敬,董鹏,施刚,等.大型双馈风电场经MMC-HVDC并网的次同步振荡及其抑制[J].中国电机工程学报,2015,35(19):4852-4860.
LÜ Jing,DONG Peng,SHI Gang,et al.Subsynchronous oscillation and its mitigation of MMC-based HVDC with large doubly-fed induction generator-based wind farm integration[J].Proceedings of the CSEE,2015,35(19): 4852-4860(in Chinese).
[8] CESPEDES M,SUN J.Impedance modeling and analysis of grid-connected voltage-source converters[J].IEEE Transactions on Power Electronics,2014,29(3): 1254-1261.
[9] 谢小荣,刘华坤,贺静波,等.电力系统新型振荡问题浅析[J].中国电机工程学报,2018,38(10):2821-2828.
XIE Xiaorong,LIU Huakun,HE Jingbo,et al.On new oscillation issues of power systems[J].Proceedings of the CSEE,2018,38(10): 2821-2828(in Chinese).
[10] 王潇,刘辉,胡小宝,等.基于等效电路阻尼稳定性判据的风电经柔性直流并网振荡风险与影响因素分析[J].全球能源互联网,2018,1(1):48-55.
WANG Xiao,LIU Hui,HU Xiaobao,et al.Analysis of risk and impacting factors of oscillation in wind farms integration via a flexible HVDC system based on equivalent circuit damping stability criterion[J].Journal of Global Energy Interconnection,2018,1(1): 48-55(in Chinese).
[11] AMIN M,MOLINAS M.Understanding the origin of oscillatory phenomena observed between wind farms and HVdc systems[J].IEEE Journal of Emerging and Selected Topics in Power Electronics,2017,5(1): 378-392.
[12] 张冲,王伟胜,何国庆,等.基于序阻抗的直驱风电场次同步振荡分析与锁相环参数优化设计[J].中国电机工程学报,2017,37(23):6757-6767.
ZHANG Chong,WANG Weisheng,HE Guoqing,et al.Analysis of sub-synchronous oscillation of full-converter wind farm based on sequence impedance and an optimized design method for PLL parameters[J].Proceedings of the CSEE,2017,37(23): 6757-6767(in Chinese).
[13] LYU J,CAI X,AMIN M,et al.Sub-synchronous oscillation mechanism and its suppression in MMC-based HVDC connected wind farms[J].IET Generation,Transmission & Distribution,2018,12(4): 1021-1029.
[14] 郭贤珊,李云丰,谢欣涛,等.直驱风电场经柔直并网诱发的次同步振荡特性[J].中国电机工程学报,2020,40(4):1149-1160.
GUO Xianshan,LI Yunfeng,XIE Xintao,et al.Subsynchronous oscillation characteristics caused by PMSGbased wind plant farm integrated via flexible HVDC system[J].Proceedings of the CSEE,2020,40(4):1149-1160(in Chinese).
[15] 李光辉,王伟胜,郭剑波,等.风电场经MMC-HVDC送出系统宽频带振荡机理与分析方法[J].中国电机工程学报,2019,39(18):5281-5297.
LI Guanghui,WANG Weisheng,GUO Jianbo,et al.Broadband oscillation mechanism and analysis for wind farm integration through MMC-HVDC system[J].Proceedings of the CSEE,2019,39(18): 5281-5297(in Chinese).
[16] CHEAH-MANE M,SAINZ L,LIANG J,et al.Criterion for the electrical resonance stability of offshore wind power plants connected through HVDC links[J].IEEE Transactions on Power Systems,2017,32(6): 4579-4589.
[17] CHEAH-MANE M,LIANG J,JENKINS N,et al.Electrical resonance instability study in HVDC-connected offshore wind power plants[C]//2016 IEEE Power and Energy Society General Meeting(PESGM),July 17-21,2016.Boston,MA,USA.IEEE,2016.
[18] 李英彪,卜广全,王姗姗,等.张北柔直电网工程直流线路短路过程中直流过电压分析[J].中国电机工程学报,2017,37(12):3391-3399.
LI Yingbiao,BU Guangquan,WANG Shanshan,et al.Analysis of DC overvoltage caused by DC short-circuit fault in Zhangbei VSC-based DC grid[J].Proceedings of the CSEE,2017,37(12): 3391-3399(in Chinese).
[19] 谢小荣,刘华坤,贺静波,等.新能源发电并网系统的小信号阻抗/导纳网络建模方法[J].电力系统自动化,2017,41(12):26-32.
XIE Xiaorong,LIU Huakun,HE Jingbo,et al.Small-signal impedance/admittance network modeling for grid-connected renewable energy generation systems[J].Automation of Electric Power Systems,2017,41(12): 26-32(in Chinese).
[20] ZHANG C,CAI X,RYGG A,et al.Sequence domain SISO equivalent models of a grid-tied voltage source converter system for small-signal stability analysis[J].IEEE Transactions on Energy Conversion,2018,33(2): 741-749.
